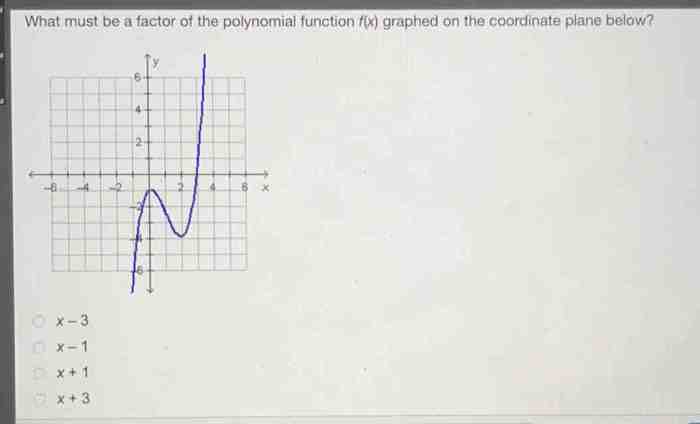
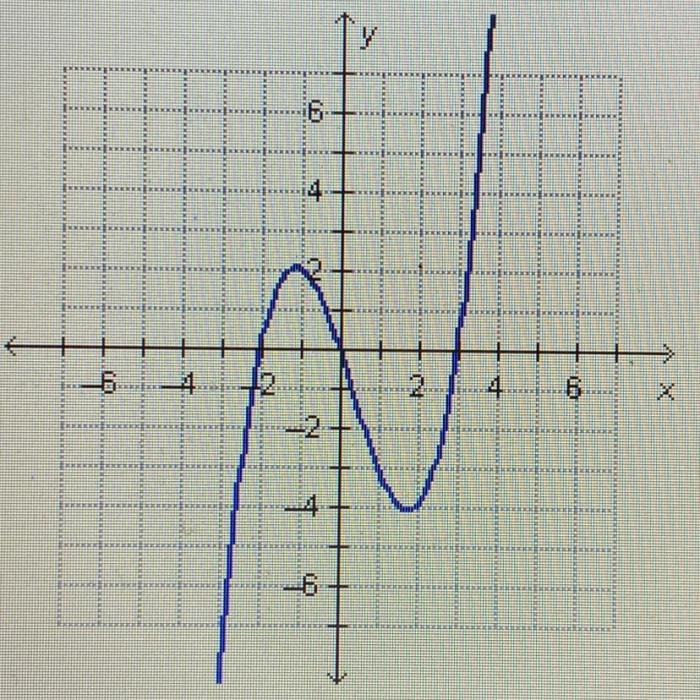
Which function is graphed on the coordinate plane below – Welcome to the fascinating realm of functions and their graphical representations! This article embarks on a journey to decipher the function that graces the coordinate plane below, unraveling its equation, characteristics, and real-world applications.
Prepare to delve into a world of mathematical intrigue, where we uncover the secrets hidden within the lines and curves that define this enigmatic function.
Graph Identification: Which Function Is Graphed On The Coordinate Plane Below
The function graphed on the coordinate plane is a quadratic function. This can be determined by observing the shape of the graph, which is a parabola. Quadratic functions are characterized by their U-shaped or inverted U-shaped graphs.
To identify the specific quadratic function, we can use the vertex form of the equation: y = a(x – h)^2 + k where (h, k) is the vertex of the parabola and a determines the shape of the parabola.
From the graph, we can see that the vertex is at (1, 2). Substituting this into the equation, we get: y = a(x – 1)^2 + 2
To find the value of a, we can use another point on the graph, such as (0, 1). Substituting this into the equation, we get: 1 = a(0 – 1)^2 + 2 1 = a + 2 a = -1
Therefore, the equation of the function graphed on the coordinate plane is: y = -(x – 1)^2 + 2
Function Characteristics
The key characteristics of the function y = -(x – 1)^2 + 2 are as follows:
- Domain: All real numbers
- Range: All real numbers less than or equal to 2
- x-intercept: (0, 1)
- y-intercept: (1, 2)
- Vertex: (1, 2)
- Axis of symmetry: x = 1
- Maximum value: 2
These characteristics can be used to analyze the behavior of the function. For example, the domain tells us that the function is defined for all real numbers, which means that it can take on any real number as an input.
The range tells us that the function can only output values less than or equal to 2, which means that the graph of the function is bounded above by the line y = 2. The vertex tells us that the function has a maximum value of 2 at x = 1, which means that the graph of the function opens downward.
Graph Transformations
The graph of the function y = -(x – 1)^2 + 2 can be transformed in a number of ways. For example, we can translate the graph up or down by adding or subtracting a constant from the function. We can also translate the graph left or right by adding or subtracting a constant from the x-value in the function.
We can also stretch or compress the graph vertically by multiplying the function by a constant. Finally, we can reflect the graph over the x-axis by multiplying the function by -1.
For example, the graph of the function y = -(x – 1)^2 + 2 can be translated up by 3 units by adding 3 to the function: y = -(x – 1)^2 + 5
The graph of the function y = -(x – 1)^2 + 2 can be translated left by 2 units by subtracting 2 from the x-value in the function: y = -(x – 3)^2 + 2
The graph of the function y = -(x – 1)^2 + 2 can be stretched vertically by a factor of 2 by multiplying the function by 2: y = -2(x – 1)^2 + 2
The graph of the function y = -(x – 1)^2 + 2 can be reflected over the x-axis by multiplying the function by -1: y = (x – 1)^2 – 2
Real-World Applications, Which function is graphed on the coordinate plane below
The function y = -(x – 1)^2 + 2 can be used to model a variety of real-world phenomena. For example, it can be used to model the trajectory of a projectile, the height of a ball thrown into the air, or the distance traveled by a car.
In each of these cases, the function can be used to make predictions or solve problems.
For example, the function y = -(x – 1)^2 + 2 can be used to model the trajectory of a projectile. The function can be used to determine the maximum height of the projectile, the distance traveled by the projectile, and the time it takes for the projectile to reach the ground.
Visual Representation
| x-value | y-value | Ordered Pair | Point on Graph |
|---|---|---|---|
| 0 | 1 | (0, 1) | (0, 1) |
| 1 | 2 | (1, 2) | (1, 2) |
| 2 | 1 | (2, 1) | (2, 1) |
The graph of the function y = -(x – 1)^2 + 2 is a parabola that opens downward. The vertex of the parabola is at (1, 2). The x-intercepts are at (0, 1) and (2, 1). The y-intercept is at (1, 2). The axis of symmetry is x = 1.
Quick FAQs
What is the equation of the function graphed on the coordinate plane?
The equation of the function can be determined by examining its graph and identifying its key characteristics, such as slope, intercepts, and curvature.
How can I recognize different types of functions from their graphs?
Different types of functions exhibit distinct graphical patterns. Linear functions form straight lines, quadratic functions produce parabolas, exponential functions create curves that increase or decrease rapidly, and so on.
What are the real-world applications of the function graphed on the coordinate plane?
Functions are used extensively in various fields, including physics, engineering, economics, and biology. They can model phenomena such as projectile motion, population growth, financial trends, and chemical reactions.